كيف نحصل على قطع مكافئ من الطبيعة

وللعلم

في التحليل الرياضي القطوع المخروطية، هو المحل الهندسي لنقطة تتحرك بحيث تكون النسبة بين بعدها عن نقطة ثابتة وبعدها عن مستقيم ثابت تساوي نسبة ثابتة. تسمى هذه النسبة الإختلاف المركزي (Eccentricity)، كما تسمى النقطة الثابتة البؤرة (Focus)، أما المستقيم الثابت فيدعى الدليل (directrix).
PS = e.PM
حيث:
– P هي نقطة (x,y) تقع على القطع
– S البؤرة
– e معامل الاختلاف المركزي
– و m هي مسقط العمودي ل P على الدليل
إذا كان الإختلاف المركزي مساويا للوحدة (عدد الواحد الصحيح) سمي المنحنى قطعا مكافئا (Parabola)، وإذا كان الإختلاف المركزي أقل من الوحدة (الواحد الصحيح) سمي المنحنى قطعا ناقصا (Ellipse)، وإذا كان الإختلاف المركزي أكبر من الوحدة(الواحد) سمي المنحنى قطعا زائدا(Hyperbola).
وتسمى القطوع المكافئة والناقصة والزائدة بالقطوع المخروطية، لأنه يمكن أن تتولد نتيجة قطع السطح المخروطي بمستو في وضع معين.
[عدل] أنواع القطوع المخروطية

لها ثلاثة أنواع هي القطع المكافئ(شلجم)، الزائد(هذلول)،والناقص(اهليج). وقد تعتبر الدائرة نوعاً رابعاً (كما اعتبرها أبولونيو)أو بمكن اعتبارها نوع من القطوع الناقصة. يتشكل القطع الناقص والدائرة عندما يكون تقاطع المستوى والمخروط منحنى مغلق. تتشكل الدائرة عندما يكون المستوى القاطع موازيً لدائرة القاعدة المولدة للمخروط- بالنسبة لمخروط يميني (كما في الشكل المقابل في أعلى الصورة) يكون المستوى القاطع عمودياً على محور تماثل المخروط.إذا كان المستوى القاطع موازي لخط واحد فقط من الخطوط المولدة للمخروط حينها يصبح القطع مفتوحاً وليس مغلقاً فيسمى قطعاً مكافئاً. وفي الحالة الأخيرة يتكون القطع الزائد عندما يتقاطع المستوى مع نصفي المخروط الإثنين ، مكوناً بذلك منحنيين منفصلين ومفتوحين ، يتم في الغالب تجاهل أحدهما والعمل بالآخر.

حالات شاذة

يوجد عدد من الحالات الشاذة تحدث عندما يمر المستوى القاطع برأس المخروط Apex. التقاطع في هذه الحالات قد يكون خطاً مستقيما ً(إذا كان المستوى مماساً لسطح المخروط)؛ أو نقطة( إذا كان الزاوية بين المستوى ومحور المخروط أكبر من المماس)؛ أو زوج من الخطوط المتقاطعة (عندما تكون الزاوية أصغر).
عندما يصبح المخروط أسطوانة -عندما يكون الرأس واقع في منطقة اللانهاية نتحصل على قطوع أسطوانية. بالرغم من أن ذلك يتسبب غالباً في قطع ناقص أو دائرة، إلا ان هناك حالة شاذة تنتج خطين متوازيين.

الإختلاف المركزي

انظر أيضاً: لا مركزية (رياضيات)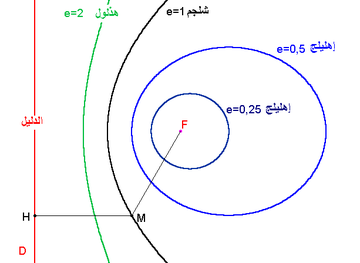
شروط التعريف الأربعة الواردة أعلاه يمكن جمعها في شرط واحد يعتمد على نقطة افتراضية F(البؤرة) ومستقيم L (الدليل)لا يمر بـ Fوعدد حقيقي غير سالب e (معامل الإختلاف المركزي).القطع المخروطي المقابل يتكون من جميع النقاط التي تبعد عن F مسافةً تساوي e مرة بعدها عن L. إذا كانت e بين 0 و 1 نحصل على قطع ناقص،إذا كانت e=1 نتحصل على قطع مكافئ وإذا كانت أكبر من 1 نحصل على قطع زائد.
هناك دليلين وبؤرتين لكل من القطع الزائد والناقص. المسافة من المركز إلى الدليل هي a / e ، بينما هو المحور شبه الأكبر– semi-major axis – للقطع الناقص، أو المسافة من المركز إلى قمة القطع الزائد. المسافة من المركز للبؤرة هي .
في حالة الدائرة يكون معامل الإختلاف المركزي e= 0 ويمكن تخيل أن الدليل قد تم استبعاده لانهائياً عن المركز. لكن من غير المفيد استخدام التعبير: ان الدائرة تتكون من كل النقاط التي التي تبعد مسافة e مرة بعدها عن L لأننا سنحصل على 0 ضرب مالانهاية!
لذلك فإن الإختلاف المركزي للقطع المخروطي هو مقياس يبين لأي مدى يبعد القطع عن أن يكون دائرة. لقيمة معطاة ، كلما اقتربت من 1 كلما نقص طول المحور شبه الأصغر semi-minor axis.